6 - Численное интегрирование функциии

Лабораторная работа 6 для студентов курса “Основы программирования” 1 курса кафедры ИУ5 МГТУ им Н.Э. Баумана.

Содержание

Цель работы

На примере разработки программы для численного интегрирования функции с заданной точностью методом прямоугольников и методом трапеций освоить следующие приемы программирования:

Начало работы

Зайдите в свою локальную директорию с репозиторием для выполнения лабораторных работ. Заберите ветку с соответствующей лабораторной работой из общего репозитория (в лабораторной работе 0 был отмечен меткой upstream):

git pull upstream

или

git pull upstream lab_6

Переключитесь на ветку с текущей лабораторной работой:

git checkout lab_6

Свяжите ветку локального репозитория с вашим удаленным репозиторием:

git push --set-upstream origin lab_6

Задание

  1. Численное интегрирование функции с заданной точностью методом прямоугольников.

    Вычислить определённый интеграл в пределах от a до b для четырех функций:

    • f₁(x) = x
    • f₂(x) = sin(22 * x)
    • f₃(x) = x⁴
    • f₄(x) = arctg(x)

    Вычисление интеграла оформить в виде функции integrationByRectangle.

    Вычисления выполнить для пяти значений точности: 0.01, 0.001, 0.0001, 0.00001 и 0.000001.

    Исследовать быстродействие алгоритма в зависимости от подынтегральной функции и требуемой точности (быстродействие алгоритма можно оценить числом элементарных прямоугольников n).

    Результаты представить в виде 5 таблиц, по одной таблице для каждого значения точности. В каждой таблице выводить данные для всех четырех функций.

    Для печати таблицы результатов использовать функцию printTabl(resultToPrint* i_prn, int countRowOfTable); , приведенную в приложении 2.

    Здесь i_prn – массив структур типа resultToPrint размерностью countRowOfTable

    Вид таблицы приведен в Приложении 1

  2. Выполнить п.1, используя для интегрирования метод трапеций. Вычисление интеграла оформить в виде функции integrationByTrapezoidal.

    3. Для печати таблиц результатов использовать ту же функцию, что и в методе прямоугольников.

Указания по выполнению работы

Алгоритм метода Дарбу-Римана аналогичен методу прямоугольников, но на каждом шаге вычисляются две суммы — верхняя (S2) и нижняя (S1):


      f1 = f(x);                    // левая граница
      f2 = f(x + dx);               // правая граница

      if (f1 <= f2) {
          S1 += f1 * dx;            // нижняя сумма
          S2 += f2 * dx;            // верхняя сумма
      } else {
          S2 += f1 * dx;
          S1 += f2 * dx;
      }

Вычисления прекращаются при |S2 - S1| < eps.

Задача вычисления определенного интеграла в пределах от a до b формулируется следующим образом: вычислить \( \int_{a}^{b} f(x)\,dx \) для подынтегральный функции f(x) при заданных значениях пределов интегрирования a, b и требуемой точности eps .

При численном интегрировании площадь под кривой заменяется суммой площадей «элементарных» прямоугольников с высотой, проведенной из середины основания.

Формула приближенного значения определенного интеграла представляется в виде:

$$ \sum_{i=1}^{N} f(x_i)Δx $$

где:

\( x_i = a + Δx/2 + (i-1)Δx \);

N - число элементарных прямоугольников.

Для уменьшения объема вычислений множитель Δx следует вынести за знак суммы. Тогда в цикле нужно выполнять только суммирование, а затем полученную сумму один раз умножить на Δx.

Для оценки погрешности вычисления интеграла на практике используют правило Рунге. Суть правила состоит в том, что выполняют вычисление интеграла с двумя разными шагами изменения переменной х, а затем сравнивают результаты и получают оценку точности. Наиболее часто используемое правило связано с вычислением интеграла дважды: с шагом Δx и шагом Δx/2.

Для методов прямоугольников и трапеций погрешность \( R_{\Delta x/2} \) вычисления интеграла с шагом Δx/2 оценивается следующей формулой:

\( \left| R_{\Delta x/2} \right| = \frac{ \left| I_{\Delta x/2} - I_{\Delta x} \right| }{3} \) , (1)

где \( I_{\Delta x/2} \) – значение интеграла, вычисленное с шагом Δx/2; \( I_{\Delta x} \) – значение интеграла, вычисленное с шагом Δx.

В программе вычисления интеграла с точностью eps во внутреннем цикле находят значение определенного интеграла с шагом Δx/2. Во внешнем цикле производится сравнение значений интегралов, вычисленных с шагами Δx и Δx/2 соответственно. Если требуемая точность не достигнута, то число разбиений удваивается, а в качестве предыдущего значения интеграла берут текущее и вычисление интеграла выполняется при новом числе разбиений.

Вычисление интеграла оформить в виде функции integrationByRectangle, формальными параметрами которой являются:

Функция возвращает значение интеграла.

Прототип функции:


  typedef double (*TPF)(double);
  double integrationByRectangle(TPF f, double a, double b, double eps, int& n);

Здесь: TPF – тип указателя на подынтегральную функцию

Для хранения и печати результатов вычислений используйте структуру, элементами которой являются наименование функции, значения интеграла (точное и вычисленное в виде суммы) и число «элементарных» прямоугольников n, при котором достигнута требуемая точность. Точные значения, полученные аналитически, нужны для оценки правильности результатов численного интегрирования.

Так как в лабораторной работе требуется выполнять вычисление интеграла для четырех функций, для пяти значений точности для каждой функции и двумя методами, то для сокращения объема программы следует использовать циклы, а для обеспечения возможности реализации циклов обрабатываемые данные нужно хранить в массивах (массив указателей на функции, массив значений точности, массив структур для хранения и печати результатов вычислений).

Aлгоритм метода трапеций аналогичен алгоритму метода прямоугольников, только площадь элементарной трапеции вычисляется по формуле: Sт=dx*(f(x)+f(x+dx))/2.

При этом значения функций на границах внутренних отрезков при вычислении интеграла используются дважды, а на границах интервала [a, b] - только один раз.

Прототип функции трапеций

double integrationByTrapezoidal(TPF f, double a, double b, double eps, int& n);

Формулы для вычисления точных значений интеграла

\( \int_{a}^{b} x\,dx \) = (b*b - a*a)/2.0

\( \int_{a}^{b} sin(22*x)\,dx \) = (cos(a*22.0) - cos(b*22.0)) / 22.0

\( \int_{a}^{b} x⁴\,dx \) = (b⁵ - a⁵) / 5.0

\( \int_{a}^{b} arctg(x)\,dx \) = b*atan(b) - a*atan(a) - (log(b²+1) - log(a²+1)) / 2.0

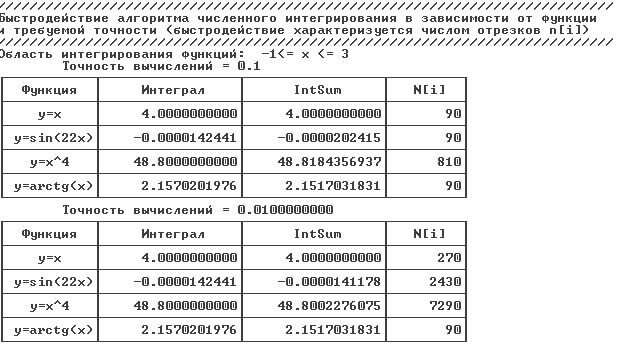
Приложение 1: Пример вывода таблицы результатов

Пример вывода таблицы результатов

Приложение 2: функция вывода таблицы


namespace {
    const int numberOfTableColumns = 4;
    const int maxWidthOfTableColumns = 18;

    const int firstColumnWidth = 12;
    const int secondColumnWidth = 18;
    const int thirdColumnWidth = 18;
    const int fourthColumnWidth = 10;

   // Символы рамки в UTF-8
    const char* ul = "┌";   // верхний левый угол		  char(218)
    const char* ur = "┐";   // верхний правый угол	  char(191)
    const char* dl = "└";   // нижний левый угол		  char(192)
    const char* dr = "┘";   // нижний правый угол		  char(217)
    //const std::string hz = u8"─"; // горизонтальная линия	char(196)
    const char* vt = "│";   // вертикальная линия		  char(179)
    const char* cr = "┼";   // перекрестие			      char(194)
    const char* Td = "┬";   // Т-образный вниз		    char(197)
    const char* Tu = "┴";   // Т-образный вверх		    char(193)
    const char* Tr = "├";   // Т-образный вправо		  char(195)
    const char* Tl = "┤";   // Т-образный влево		    char(180)
}

struct resultToPrint {
    char* name;      // название функции
    double i_sum;    // численно рассчитанный интеграл
    double i_toch;   // точное значение интеграла
    int n;           // число разбиений при достижении точности
};

void printTabl(resultToPrint* i_prn, int countRowOfTable)
{
    int widthOfTableColumns[numberOfTableColumns] = {
        firstColumnWidth, secondColumnWidth,
        thirdColumnWidth, fourthColumnWidth
    };

    char* title[numberOfTableColumns];
    title[0] = new char [std::strlen("  Function  ") + 1];
    std::strcpy(title[0], "  Function  ");
    title[1] = new char [std::strlen("     Integral     ") + 1];
    std::strcpy(title[1], "     Integral     ");
    title[2] = new char [std::strlen("      IntSum      ") + 1];
    std::strcpy(title[2], "      IntSum      ");
    title[3] = new char [std::strlen("    N     ") + 1];
    std::strcpy(title[3], "    N     ");

    int size[numberOfTableColumns];
    for(int i = 0; i < numberOfTableColumns; ++i)
        size[i] = std::strlen(title[i]);

    // Верхняя рамка
    std::cout << ul << std::setfill('-');
    for(int j = 0; j < numberOfTableColumns - 1; ++j)
        std::cout << std::setw(widthOfTableColumns[j] + 3) << Td;
    std::cout << std::setw(widthOfTableColumns[numberOfTableColumns - 1] + 3) << ur << std::endl;

    // Заголовки
    std::cout << vt;
    for(int j = 0; j < numberOfTableColumns; ++j)
        std::cout << title[j] << vt;
    std::cout << std::endl;

    // Тело таблицы
    for(int i = 0; i < countRowOfTable; ++i)
    {
        std::cout << Tr << std::setfill('-');
        for(int j = 0; j < numberOfTableColumns - 1; ++j)
            std::cout << std::setw(widthOfTableColumns[j] + 3) << cr;
        std::cout << std::setw(widthOfTableColumns[numberOfTableColumns - 1] + 3)
                  << Tl << std::setfill(' ') << std::endl;

        std::cout << vt
                  << std::setw((widthOfTableColumns[0] - std::strlen(i_prn[i].name)) / 2) << ' '
                  << i_prn[i].name
                  << std::setw((widthOfTableColumns[0] - std::strlen(i_prn[i].name)) / 2) << vt;

        std::cout << std::setw(widthOfTableColumns[1]) << std::setprecision(6)
                  << i_prn[i].i_toch << vt
                  << std::setw(widthOfTableColumns[2])
                  << i_prn[i].i_sum << vt
                  << std::setw(widthOfTableColumns[3])
                  << i_prn[i].n << vt << std::endl;
    }

    // Нижняя рамка
    std::cout << dl << std::setfill('-');
    for(int j = 0; j < numberOfTableColumns - 1; ++j)
        std::cout << std::setw(widthOfTableColumns[j] + 3) << Tu;
    std::cout << std::setw(widthOfTableColumns[numberOfTableColumns - 1] + 3)
              << dr << std::setfill(' ') << std::endl;

   // Освобождение памяти
    for (int i = 0; i < numberOfTableColumns; ++i)
        delete[] title[i];
}

Структуры в С++

В программировании часто бывает так, что для представления чего-либо требуется более одной переменной. Допустим, мы хотим написать программу для хранения информации о сотрудниках компании. Нам может быть интересно отслеживать такие атрибуты, как имя сотрудника, должность, возраст, идентификатор сотрудника, идентификатор руководителя, заработную плату, день рождения, дату приёма на работу и т. д. Если бы мы использовали независимые переменные для отслеживания всей этой информации, это могло бы выглядеть примерно так:

char* name;
char* title;
int age;
int id;
int managerId;
double wage;
int birthdayYear;
int birthdayMonth;
int birthdayDay;
int hireYear;
int hireMonth;
int hireDay;

Однако такой подход сопряжен с рядом проблем. Во-первых, не сразу понятно, связаны ли эти переменные на самом деле (придётся читать комментарии или смотреть, как они используются в контексте). Во-вторых, теперь нужно управлять 12 переменными. Если бы мы захотели передать этого сотрудника в функцию, нам пришлось бы передать 12 аргументов (причём в правильном порядке), что привело бы к путанице в прототипах и вызовах функций. А поскольку функция может возвращать только одно значение, как функция вообще может возвращать сотрудника? А если бы нам понадобилось больше одного сотрудника, нам пришлось бы определить ещё 12 переменных для каждого дополнительного сотрудника (каждой из которых потребовалось бы уникальное имя)! Это, очевидно, совершенно не масштабируется. Нам действительно нужен способ организовать все эти связанные данные вместе, чтобы ими было проще управлять.

К счастью, в C++ есть два составных типа данных, предназначенных для решения таких задач: структуры (с которыми мы познакомимся сейчас) и классы (которые мы рассмотрим вскоре). Структура (struct) — это программно-определяемый тип данных ( 13.1 — Введение в программно-определяемые (пользовательские) типы ), позволяющий объединять несколько переменных в один тип. Как вы скоро увидите, это значительно упрощает управление связанными наборами переменных!

Cтруктуры — это программно-определяемый тип, нам сначала нужно сообщить компилятору, как выглядит наш структурный тип, прежде чем мы сможем его использовать. Вот пример определения структуры для упрощённого сотрудника:

struct Employee {
    int id {};
    int age {};
    double wage {};
};

Ключевое struct слово используется для того, чтобы сообщить компилятору, что мы определяем структуру, которой мы дали имя Employee (поскольку определяемым программой типам обычно даются имена, начинающиеся с заглавной буквы).

Затем, в фигурных скобках, мы определяем переменные, которые будет содержать каждый объект Employee. В этом примере каждый Employeeсоздаваемый нами объект будет содержать три переменные: int id, int age и double wage. Переменные, входящие в структуру, называются элементами данных (или переменными-членами).

Чтобы использовать Employeeтип, мы просто определяем переменную типа Employee:

Employee joe {}; // создание Employee структуры для Joe
Employee frank {}; // создание Employee структуры для Frank

Одно из самых больших преимуществ структур заключается в том, что нам нужно создать только одно новое имя для каждой переменной структуры (имена членов фиксированы как часть определения типа структуры). В следующем примере мы создаём два Employee объекта: joe и frank.

#include 

struct Employee
{
    int id {};
    int age {};
    double wage {};
};

int main()
{
    Employee joe {};
    joe.id = 14;
    joe.age = 32;
    joe.wage = 60000.0;

    Employee frank {};
    frank.id = 15;
    frank.age = 28;
    frank.wage = 45000.0;

    int totalAge { joe.age + frank.age };
    std::cout << "Joe и Frank: общее количество лет " << totalAge << '\n';

    if (joe.wage > frank.wage)
        std::cout << "Joe зарабатывает больше чем Frank\n";
    else if (joe.wage < frank.wage)
        std::cout << "Joe зарабатывает меньше чем Frank\n";
    else
        std::cout << "Joe and Frank зарабатывают одинаково\n";

    // Frank Фрэнк получил повышение
    frank.wage += 5000.0;

    // Сегодня день рождения joe
    ++joe.age;

    return 0;
}

В приведённом выше примере очень легко определить, какие переменные-члены принадлежат Джо, а какие — Фрэнку. Это обеспечивает гораздо более высокий уровень организации, чем организация отдельных переменных. Более того, поскольку члены Джо и Фрэнка имеют одинаковые имена, это обеспечивает согласованность при наличии нескольких переменных одного структурного типа.

Передача в функцию в качестве параметров одномерных массивов и имен функций

Массивы и функции передаются в функцию через указатели.

Имя массива является указателем на его нулевой элемент. Указатель «ничего не знает» о длине массива и длина массива должна передаваться в функцию как параметр.

Имя функции указывает на первую команду кода функции.

Передача одномерных массивов в функцию

#include <iostream>
int sum(int *a, int n);  // В функцию передаются указатель на начало массив(имя массива a) и его размерность(n)

int main() {
    int n;
    int a[] = {1,2,3,4,5,6,7,8};
    n = sizeof(a)/sizeof(int);  // Определение размерности инициализированного массива
    std::cout << "n = " << n << std::endl;
    std::cout << sum(a, n) << std::endl;
    return 0;
}

int sum(int* a, int n) {
    int s = 0;
    int k = sizeof(a); //k – размер указателя (4 байта)
    std::cout << " k = " << k << std::endl;
    for (int i = 0; i < n; ++i)
        s += a[i];
    return s;
}

Передача имен функций в качестве параметров


/*для удобочитаемости программы определяется новый тип
(тип пользователя) PF - указатель на функцию, которая имеет
один параметр типа int и не возвращает никакого значения*/

#include <iostream>

typedef void (*PF)(int);

void f1(PF pf) {
    pf(5);         //вызов функции через указатель
}

void f(int i) {
    std::cout << i << std::endl;
}

int main() {
    f1(f);        // Функция выведет на экран число 5
    return 0;
}

Функция f1() получает в качестве параметра указатель типа PF